Patterns in prime numbers?

This is non-science. Maybe. Maybe not: decide for yourself.

Look at this picture: Stars and stripes?. Do you see patterns in here? If so, you see patterns in the distribution of prime numbers. Come follow me into the world of prime number patterns.

Introduction|Background|Java Do-It-Yourself|C code

How was it done?

The original idea came from an article about prime number searching in the september '88 german issue of the Scientific American, Spektrum der Wissenschaft. The article briefly mentioned "[Stanislaw] Ulam's Spiral", which is a way of mapping the set N of natural numbers onto the grid N x N. Marking all prime numbers black, Ulam saw patterns emerge.

Ulam's method is a little unhandy to put into formulas; here is an easier mapping: 

 1   4   9  16  ..
   3   8  15  ..
 2   7  14  23
   6  13  22
 5  12  21  32
  ..  ..
..  ..
  ..
..
As you can easily see, any horizontal, vertical or 45-degree line corresponds to a quadratic progression, i.e. is of the form a*n^2 + b*n + c. It is therefore equivalent to ask wether certain quadratic progressions contain infinitely many primes or wether the easily spotted lines in the above picture continue forever.

What do I see?

If you look at the picture long enough, maybe looking at a shallow angle, you will see lines in more directions than just in the prominent 45 degree direction.

Of course, if you look long enough, you will see anything you want to see (including strange faces...). So how do we substantiate the feeling that there are hidden patterns?

Fourier transform

You can calculate a two-dimensional discrete fourier transform over the matrix of zeros and ones, displaying the log magnitude. This is the result for a 256x256 matrix. (Click below to load 130K jpeg picture for a 1024x1024 matrix).

Load 1024x512 jpeg picture

Notice that there appears to be some "self-similarity" in the picture: There are triangles in triangles in triangles...

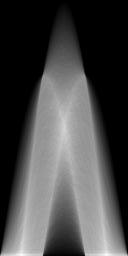
Hough transform The hough transform (picture, 2.3 kB)

To find out something about the prominent orientation of the lines, you can calculate the hough transform over the matrix. The picture on the right displays a kind of likelihood that a line exists at a given angle (left to right) and distance (bottom to top) to the origin. In the diagram, angle runs from 0 to 270 degrees.

Notice that indeed there are prominent intensity peaks at 45, 135 and 225 degrees.

What do all these pictures mean?

I don't really have a clue. Maybe you have an idea? If so, write me a mail.

For those of you who want to experiment a little more: Here is C code (gzipped, 17 KB) to generate a list of prime numbers and C code to map them onto a grid, writing out a pbm-File of the prime number distribution. You will probably need Jef Poskanzer's pbm tools to convert these files to gif or anything displayable.

If you want can't wait to compile these programs, try the JAVA Applet below.

JAVA Implementation

Unfortunately, your browser does not support Java.
Version: Saturday, 21 December 1996 19:50:23
Wolfgang Schildbach <wschildbach@fermi.franken.de>